各位早安。今天我們來註解一下，歐幾里得平面幾何大師的一首詩。
109Please respect copyright.ＰＥＮＡＮＡEvBGgKrudN
開門見山，這首詩一開始有兩個集合，一個是「我」，一個是「妳」。而我們分析的元素，主要在 ℝ² 以2元組表示，即是 x-y 座標平面上的座標。
109Please respect copyright.ＰＥＮＡＮＡFVliXTFV6H
致原在X軸上，至今卻已不在同象限的妳
109Please respect copyright.ＰＥＮＡＮＡIAR5xjDjus
從第一分句，可以推斷集合「妳」的所有元素都在X軸上。
109Please respect copyright.ＰＥＮＡＮＡhTTB1UvG37
設「妳」= { ∀(x,y) ∈ ℝ² | y = 0 }，109Please respect copyright.ＰＥＮＡＮＡHATfrFRWnK
即「妳」是所有y座標 = 0 的點的集合。
109Please respect copyright.ＰＥＮＡＮＡbs8Cbk0WLl
從第二分句，知道了「妳」變化為完全在另一個象限的集合。顯然的，這是由於函數映射所致，但我們尚未知道是特定哪個象限。我們可以將其命名為「妳*」以便理解。
109Please respect copyright.ＰＥＮＡＮＡbc2yjwOPMG
將此函數命名為 f。設f : ℝ → ℝ²，於函數 f(x) 輸入所有「妳」的元素的 x 座標，可以得到「妳*」。
109Please respect copyright.ＰＥＮＡＮＡRVCzL8rluz
另外，我們推斷出「我」、「妳*」的兩個共同性質：
1. x,y ≠ 0 ∀ (x,y) ∈「我」或「妳*」，109Please respect copyright.ＰＥＮＡＮＡuX0fmZpIZ0
即「我」、「妳*」沒有任何一個元素位於 x 或 y 軸。
2. ∄ (x₁,y₁),(x₂,y₂) ∈「我」或「妳*」 x₁ > 0 > x₂ ∨ y₁ > 0 > y₂，109Please respect copyright.ＰＥＮＡＮＡZLzRGT1mX8
即它們各自的所有元素都只存在在某一個單一象限
3. ∀ (x₁,y₁) ∈「我」且 ∀ (x₂,y₂) ∈「妳*」，109Please respect copyright.ＰＥＮＡＮＡdji3g8EHFK
sgn(x₁) ≠ sgn(x₂) ∨ sgn(y₁) ≠ sgn(y₂)109Please respect copyright.ＰＥＮＡＮＡQZf7Upgpnw
，即「我」、「妳*」不存在於同一象限。
109Please respect copyright.ＰＥＮＡＮＡJpvS0OICBV
平行時的這兩年，我們的距離一直沒變
很一般的做同學，帶姓喊你不敢逾越
我應該再出格一點，讓斜率多幾倍
我們就能擺脫平行線，在遠處重疊？
109Please respect copyright.ＰＥＮＡＮＡDn5ApAbAKS
此處指出，「我」、「妳*」是一對不相交的平行線。首先，「線」指出了兩個重要的，「我」、「妳*」共同滿足的性質。109Please respect copyright.ＰＥＮＡＮＡD6hhgpndWi
∀ (x₀,y₀),(x₁,y₁),(x₂,y₂) ∈「我」且109Please respect copyright.ＰＥＮＡＮＡHMlLP2LuVi
∀ (x₀,y₀),(x₁,y₁),(x₂,y₂) ∈「妳*」，109Please respect copyright.ＰＥＮＡＮＡqyJA1DUyHb
即對於「我」或「妳*」的所有元素：
1. 線性：(x₁ - x₂)(y₀ - c) = (y₁ - y₂)x₀，其中 c ∈ ℝ，109Please respect copyright.ＰＥＮＡＮＡcGktQKtoGg
即 c，y 截，是任意實數。
2. 稠密性：∃ (x,y) ∈「我」、「妳*」 x₁ < x < x₂ ∧ y₁ < y < y₂，109Please respect copyright.ＰＥＮＡＮＡaH5ZuLfi8P
即在兩個元素之間，必然有一個元素。
109Please respect copyright.ＰＥＮＡＮＡZCoJJtrgOq
其次，一對不相交的平行線，代表「我」、「妳*」滿足以下兩個性質。109Please respect copyright.ＰＥＮＡＮＡjI52a4kY7v
∀ (x₁,y₁),(x₂,y₂) ∈「我」且109Please respect copyright.ＰＥＮＡＮＡEmKIHxzkic
∀ (x₃,y₄),(x₄,y₄) ∈「妳*」，109Please respect copyright.ＰＥＮＡＮＡeketuvVELL
即對於「我」或「妳*」的所有元素：
1. 「我」∩「妳*」= ∅，109Please respect copyright.ＰＥＮＡＮＡ6jWojMTLCr
即「我」和「妳*」的交集是空集，即沒有交點。
2. m = (y₁ - y₂) / (x₁ - x₂) = (y₃ - y₄) / (x₃ - x₄) ∨ ( x₁ = x₂ ∧ x₃ = x₄)，109Please respect copyright.ＰＥＮＡＮＡ6sjR2yY0pC
即除非是垂直線，否則兩者斜率 m 相同。
109Please respect copyright.ＰＥＮＡＮＡEppZT2Ni3y
所以，我們可以用線性方程的形式表達「我」、「妳*」。109Please respect copyright.ＰＥＮＡＮＡrHcHhb1Nnz
∀ x,y ∈ ℝ，109Please respect copyright.ＰＥＮＡＮＡdLsCSm62IV
即對於所有實數 x，y：
「我」：a(y - c₁) = bx
「妳*」：a(y - c₂) = bx
其中 a,b,c₁,c₂ ∈ ℝ，109Please respect copyright.ＰＥＮＡＮＡDcoCfxvjBs
即 a，b、c₁、c₂ 是任意實數；109Please respect copyright.ＰＥＮＡＮＡIMJDPlJ8Et
且 c₁ ≠ c₂。
109Please respect copyright.ＰＥＮＡＮＡ5bhJ57HUKm
另外，此段呼應上文「妳」，由於「妳*」是直線，可以推論「妳」本是一條位於 x 軸的直線，即 y = 0。
109Please respect copyright.ＰＥＮＡＮＡ1R4tz14ZHU
同時，此處有一個伏筆：「我」想讓自己的斜率「多幾倍」，代表不會轉換正負，從而在遠處與「妳*」重疊；但詩詞卻在最尾留了問號。那麼「我」、「妳*」的斜率，有可能相隔甚遠，或者斜率非常小，甚至是 0 或 未定義，以致於「我」的斜率未必能多幾倍；或即便「我」的斜率多幾倍，要與「妳*」相交還是很難。
109Please respect copyright.ＰＥＮＡＮＡCfohOvqFgX
綜合以上線索，估算其中一個可能：109Please respect copyright.ＰＥＮＡＮＡ7iAJCDlscv
「我」： y = -C，109Please respect copyright.ＰＥＮＡＮＡsfyu32S3EK
而「妳*」：y = C，109Please respect copyright.ＰＥＮＡＮＡQ4JxBzlvmp
其中 C 是任意正實數。
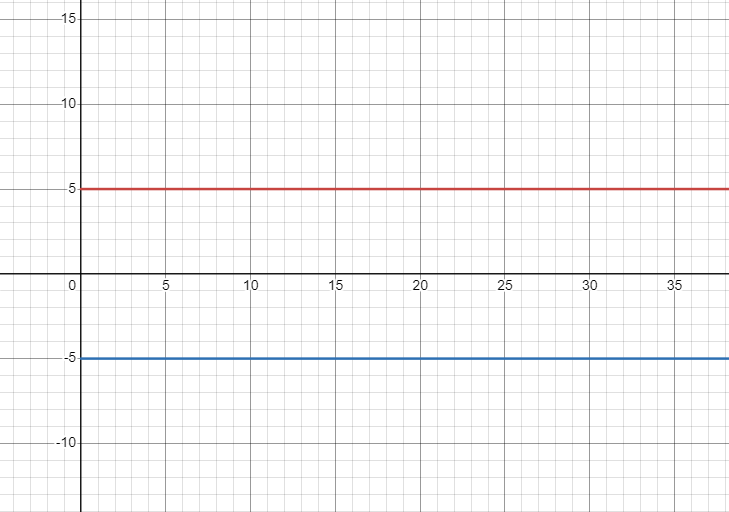
藍線的「我」如果斜率上升，便有機會在遠處與紅線的「妳*」交會；但「我」的斜率明顯為 0，這是考慮到上文提及的詩詞中的伏筆。
109Please respect copyright.ＰＥＮＡＮＡrK0rco0YxU
開始漸進的這一年，抱歉我已多設立了一個軸線
注定不可能的曲線，原諒我漸近線本就靠兩邊
與原點漸行漸遠，兩軸卻都不見交會的點
我應該選擇專心靠向妳這邊
109Please respect copyright.ＰＥＮＡＮＡSvGzjXVGBV
此處軸線應指對稱軸，可以想像「我」具有某種對稱性，109Please respect copyright.ＰＥＮＡＮＡr1oFwEKj0C
亦即可以透過代入 x = g(u)，讓 f(g(u)) 成為偶函數。
109Please respect copyright.ＰＥＮＡＮＡda77q7N2GN
重溫偶函數的定義：
f(-x) = f(x)
109Please respect copyright.ＰＥＮＡＮＡ76oSqIqbzJ
漸近線「靠兩邊」，但「兩軸卻都不見交會的點」，這給了一個很明確的限定範圍：「我」的對稱軸與漸近線都不能與「妳*」交會。然而「我」、「妳*」本是平行線，而平行線的對稱軸垂直於自身，斜率並不相等，所以必然與自身的平行線相交。
109Please respect copyright.ＰＥＮＡＮＡFTPPMcFOlm
可以推論，「我」透過了一個函數 g : ℝ² → ℝ²，映射成為「我*」，而「我*」滿足以下性質：
1. 「我*」有漸近線，所以是曲線。
2. 「我*」的對稱軸與漸近線不與「妳*」交會。由於「妳*」只在單一象限，「我*」及其對稱軸與漸近線只能在其餘三個象限裡。
3. 對稱軸與漸近線是無限制的直線，所以至少會跨越兩個象限，呼應「原諒我漸近線本就靠兩邊」。
109Please respect copyright.ＰＥＮＡＮＡbpPpfMVJgM
暫且不為「我*」下嚴謹定義，因為接下來的詩詞為我們提供了很重要的線索。
109Please respect copyright.ＰＥＮＡＮＡeXp80vIXMO
如今我們的距離已不只是軸線，分散於一四象限
我曾試著往Y軸，卻勾不著她一丁點
回頭想繼續漸近你的軸線，卻因空間斷了線
這遙遠的距離到底要用什麼填？
109Please respect copyright.ＰＥＮＡＮＡmjtlvcHfKw
這裡交代了兩個重要的訊息：
1. 「我*」的對稱軸是另一個集合的漸近線；反之亦然。
2.「我*」「試著往Y軸，卻勾不著她一丁點」，即「我*」的漸進線是 y 軸。
109Please respect copyright.ＰＥＮＡＮＡDTxYzJdjFh
「妳*」是一條直線，唯有再透過函數映射成為「妳**」。
109Please respect copyright.ＰＥＮＡＮＡLxdnipMVHO
至此，兩者的樣貌已經明朗。我們再看看下一段。
109Please respect copyright.ＰＥＮＡＮＡnSqFB5VAbH
拜託時間再給我一次機會，返回、反悔
我將扭轉時空，扭轉命運，顛覆雙軸線
讓我們這兩點重疊，對你不再虧欠
如果可以，我將對稱到你那邊，兩點交會
109Please respect copyright.ＰＥＮＡＮＡmitJfHqpqy
「顛覆雙軸線」、「對稱到你那邊」，加上前一段「我*」「試著往Y軸，卻勾不著她一丁點」，幾乎可以肯定地下定論：
109Please respect copyright.ＰＥＮＡＮＡMPBX0qskl4
「我*」與「妳**」是沿著 y 軸對稱的兩條線。那麼兩者的函數，必定是正負對應。
109Please respect copyright.ＰＥＮＡＮＡEyNDXuqU5o
那麼「我*」對稱軸如何是「妳**」的漸近線呢？首先，兩者沿著 y 軸對稱，所以「我*」對稱軸如果是「妳**」的漸近線，那也是自己的漸近線。
109Please respect copyright.ＰＥＮＡＮＡpQTTGvZSNm
由此，我想到一個可能：
「我*」：y = - 1 / x² { x > 0 }
「妳**」：y = 1 / x² { x > 0 }
109Please respect copyright.ＰＥＮＡＮＡVQJMdMySQc
{ x > 0 } 的作用，是確保兩者停留在各自的象限；而 1 / x²，是一個很特別的函數，它是偶函數，而對稱軸亦是其漸近線。
109Please respect copyright.ＰＥＮＡＮＡHejXanw15v
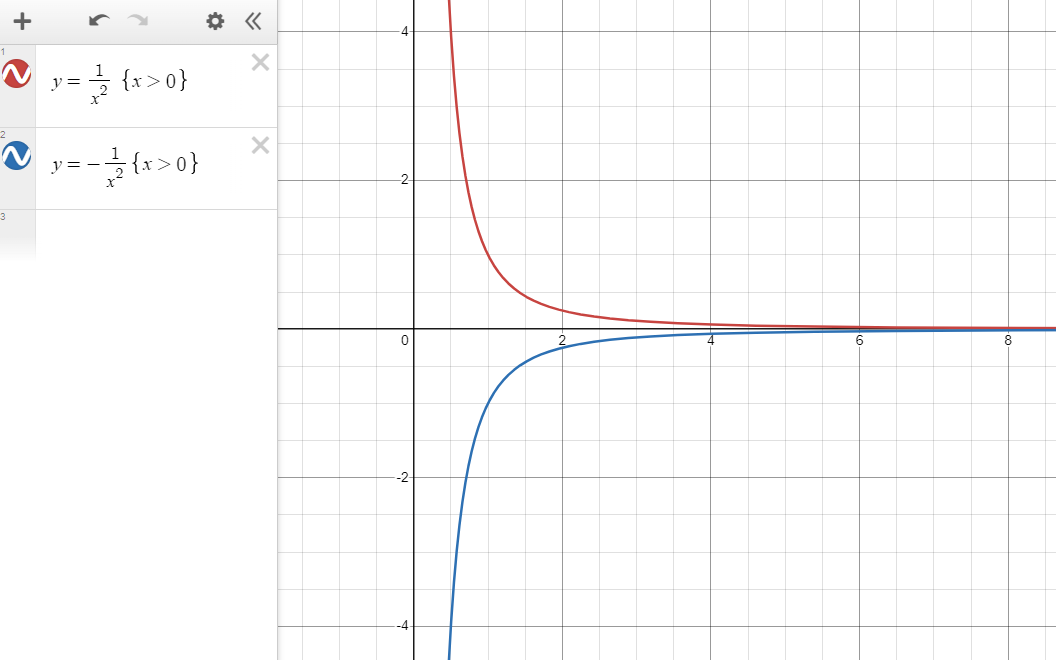
109Please respect copyright.ＰＥＮＡＮＡvsdbNIO4OZ
兩條曲線的戀愛故事，至此落幕。
109Please respect copyright.ＰＥＮＡＮＡSpPHdrtdZG
109Please respect copyright.ＰＥＮＡＮＡfnPhWA4RBq
她是天上獨異的仙子，我是地下一般的人兒。
她輕柔地滑下來，我艱苦地爬上去。
我們看到彼此，我們走向對方。
位於無窮遠處，方以無窮近對。
109Please respect copyright.ＰＥＮＡＮＡ8fL8sg8zC5
哈哈哈，玩了個雖小但長的玩笑。
109Please respect copyright.ＰＥＮＡＮＡdR7FQAS4a6
一開始看到漸近線這首詩，看到是數學的內容，心裡就有點躁動不已；再看看題目，竟然可以用詩的註解參加創挑，我就決定了，要來個大玩特玩XD
109Please respect copyright.ＰＥＮＡＮＡHNnqdcUr3U
最後的短短的詩，玩了一點寬對，希望你覺得有趣，嘿嘿。
109Please respect copyright.ＰＥＮＡＮＡ1lDDpkHeDS
本來想再寫下面第二首的，但一來有可能使得套路相似而沉悶，二來我怕趕不上，抱歉 Orz
ns 15.158.61.6da2
